Tuesday, August 4, 2020
Graph Representation
Graph Declaration
First let us look at the components of graph data structure. To
represent graphs, we need the number of vertices, the number of edges
and also their interconnections.
Adjacency Matrix
The adjacency matrix of a graph is a square matrix of size
N × N, where N is the number of Nodes of the graph.
It is basically a Boolean matrix which is initialized with zero. Let’s
Say our adjacency matrix as Adj[][]. So Adj[u][v] is set
to 1 if there is an edge between node u and v, otherwise it is zero.
Now if the graph is undirected you can either set Adj[v][u] = 1, whenever you set Adj[u][v] = 1 or you can just leave Adj[v][u] = 0. In both the cases to save time we will just process Diagonally half of this Matrix.
Now if the graph is directed you have to consider Adj[v][u] whenever you set Adj[u][v] to 1, because Adj[v][u] ≠ Adj[u][v] for directed graph. But in that case also we will just process diagonal half of the matrix as in each step when Adj[u][v] comes we will also check Adj[v][u].
The Adjacency matrix representation is good if the graphs are dense.
The matrix requires
O(N2)
bits of Storage and
O(N2)
time for Initialization. If the number of edges is proportional to
N2,then there is no problem because
N2steps are required to read the edges.
But the Downside is that it doesn’t matter the edges are minimum or maximum it will always take same amount of Space and Time. Which is why Nowadays we don’t use this kind of implementation. If N ≤ 104, we can use It, but if N ˃ 104 We can’t use this implementation in competitive coding platforms. It will give TLE error.
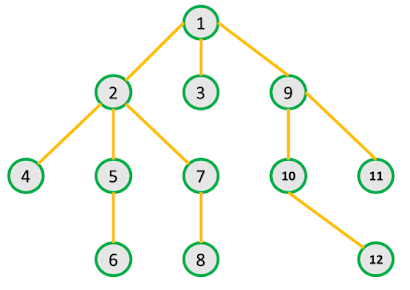
Adjacency List
Adjacency list is better implementation. The basic concept is that we create a list of node and each list node have only those nodes which are connected to the list node.
See below Images to get better idea.
One thing to be kept in mind is that the order of edges in input is important. This is because the order in which edges appear on the adjacency list affects the order in which they are processed by algorithms.
The adjacency List takes O(N+M) of space where N is number of node and M are number of edges. Which is far more less than Adjacency matrix. Also graph traversals are fast & easier in Adjacency List.
Go to the Implementation Part to Know how They are Implemented.
More Topics will be Added Soon 💚
Monday, August 3, 2020
BASIC GRAPH THEORY
BASIC GRAPH THEORY
Introduction
In the real world many problems are represented in terms of objects and
connections between them. For example, in Railway route map we might be
interested in questions like:
“What is the fastest way to go from Lucknow to Delhi?”
To answer these questions, we use Graph Data structures.
A graph is simply a way of encoding pairwise relationships among a set of
objects. It consists of a collection of V nodes and E edges. Edge
simply connects two of the nodes but not necessarily. An edge can also go
start and end on same node, these types of edges are called self-loops. We
will discuss them on later posts.
Types of Edges
· Directed Edge
- Ordered Pair of Vertices (u, v).
- First Vertex is Origin
- Second Vertex is Destination
- Its like one-way road
· Undirected Edge
- Unordered pair of vertices (u, v).
- Its like two-way road.
Types of Graphs
-
Directed Graph
- All edges are Directed
- It is like Route Network
-
Undirected Graph
- All Edges are Undirected
- Its like Flight network
Important Points You Should Know
- A degree of vertex is the number of edges incident on it.
- Two edges are parallel if they connect the same pair of vertices.
- A graph with no cycles is called a Tree. A Tree is an acyclic connected graph.
- A self-loop is an edge that connects a vertex to itself.
- Graphs with relatively few edges are called Sparse Graphs.
- A graph is connected if there is a path from every vertex to every other vertex.
- If graph is not connected, then is consists of a set of Connected Components.
- Graphs with all edges present are called Complete graphs.
- Weighted graphs have weights assigned to each edge or node.
Graphs & Algorithms
GRAPH
1) Basic Graph Theory
i) Introduction
ii) Representation
2) Graph Implementation
ii) Adjacency List
3) Graph Algorithms
4) Graph Traversal
5) Famous Problems on Graph
More topics will be made available soon💚